交易日歷
交割計算器
交割地圖
賬單查詢
電話下單
專線下單
最新保證金
最新公司標準手續(xù)費
期權作為一種金融衍生投資工具，相對于股票交易的邏輯主要是其價格的上漲和下跌, 期權具有獨特的風險收益關系，需要投資者在交易的時候同時關注期權價格與時間流逝、標的資產價格、標的資產價格的波動率這三種因素，俗稱時間、空間、波動率，之間的變化關系。剛開始接觸期權的投資者可能會認為期權交易相對復雜而很難進一步去了解，但是在真正了解了希臘字母 – 期權價格變化的影響因素，相信大家會對期權頭寸的精細化管理嘆為觀止，也為后面理解期權組合策略收益情況打好基礎。
昨天權漫畫系列六 期權希臘字母之Delta，給大家初次講解了第一個期權希臘字母的含義，今天繼續(xù)推出Gamma和Vega的詳解。
Gamma反映的是Delta對標的資產價格變動的敏感程度，即期權價格隨著標的資產價格變化的加速度，因為如果Gamma較大，標的資產價格變動的時候會帶動Delta的變化加快，進而導致期權價格的變化幅度增大。
比如對于買入平值認購期權，Delta為0.5，若Gamma為0.1，那么標的資產價格上升1元，由于Gamma的影響，導致Delta增加0.1，變成0.6，說明期權價格對標的資產的變動更加敏感。如果單看策略中的Delta，標的資產價格變動幅度不足以完全覆蓋期權價格的變動，所以Gamma是非常重要的希臘字母，衡量標的資產價格波動幅度對期權價格的影響，在期權交易中價格的波動不容忽視。
Gamma的特點：
1.對于認購和認沽期權的買方，標的資產上漲或者下跌會為投資者帶來收益，所以對于任意行權價格，Gamma大于零。
2.反之對于認購和認沽期權的賣方，對于任意行權價格，Gamma小于零。
3.當行權價格等于標的資產價格，即對于平值的認購和認沽期權來說，標的資產價格的變動對期權的性質會產生較大的影響，波動性較強，所以平值期權的Gamma相對虛值和實值期權較大。
Gamma的應用：
Gamma衡量Delta中性策略對沖的誤差/風險。
比如對于上述買入平值認購期權的案例，若標的資產價格上升1元，為了保持Delta中性策略，就不僅僅只對沖原來0.5的Delta，還需要考慮Gamma對Delta帶來的那0.1的增量。因此進行Delta中性對沖時，Gamma越大，Delta變化的就越快，對沖的風險和難度也越大，反之亦然。
Vega是衡量標的資產價格的波動率對期權價格的影響程度。即波動率上漲（下跌）1%，期權價格上漲（下跌）的變化量為Vega。無論對于認購還是認沽期權，只要是期權的買方，持有頭寸的Vega大于零，希望波動率增大；期權的賣方，持有頭寸的Vega小于零，希望波動率越小越好。
Vega是考慮波動率的變化對期權價格的影響。可能買入一個隱含波動率為20%的標的資產，價格為100元，一周后標的資產的價格還是100元，但是隱含波動率下降到15%，那么對于期權的買方，即做多Vega的一方，是虧損的。
Vega的特點：
1.對于認購和認沽期權的買方，波動率上漲會帶來收益，即Vega大于零。
2.反之對于認購和認沽期權的賣方，波動率下跌會帶來收益，所以Vega小于零
3.和Gamma的特點相似，平值期權隨著標的資產價格的變動，期權在到期是否會被行權的不確定性最大，即期權價格對標的資產價格的波動率最為敏感，所以平值期權Vega最大。
Vega的應用：
今天（11月27日）早市收盤時50ETF價格為2.993元/份，對應行權價格為3元的平值認購50ETF期權近月合約的價格為0.0028元/份，行權價格為3元的平值認沽50ETF期權近月合約的價格為0.009元/份，兩者vega均為0.0006。在50ETF價格的波動率上升（下降）1%時，平值認購和認沽期權的價格均上漲（下跌）0.0006，即平值認購期權價格上漲至0.0034元/份，或下跌至0.0022元/份；平值認沽期權價格上漲至0.0096元/份，或下跌至0.0084元/份。
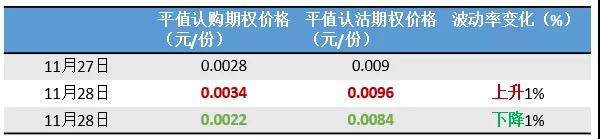
所以無論對于認購還是認沽期權，vega增加，即波動率對期權價格的影響增加，期權的價格會上漲；vega降低，即波動率對期權價格的影響降低，期權的價格會下降。
